SEMANA 12 EL MAPA FÍSICO DE ÁFRICA

HACER EL MAPA EN EL CUADERNO CON LAS DIFERENTES FORMAS DEL RELIEVE

SEMANA 11 LAS ANTIGUAS CIVILIZACIONES

ÁFRICA	EGIPTO RÍO NILO
ASIA	CHINA (RÍOS AMARILLO Y AZUL) INDIA (RÍOS GANGES Y BRAHMAPUTRA) REGIÓN DE MESOPOTAMIA (RÍOS TIGRIS Y ÉUFRATES) ARIOS, ACADIOS, ASIRIOS, HEBREOS, BABILONIOS
AMÉRICA	MAYAS (PENÍNSULA DEL YUCATÁN) INCAS (PERÚ) AZTECAS (MÉXICO)
EUROPA	GRECIA (PENÍNSULA BALCÁNICA) ROMA (PENÍNSULA ITÁLICA)
OCEANÍA	ANANGU ARUNTA KOORI

COPIAR EL ANTERIOR CUADRO EN EL CUADERNO Y APRENDERSE LOS DATOS DE MEMORIA

SEMANA # 10 FILOSOFIA

CÁTEDRA DE LA PAZ

ACTIVIDADES

• 1. Los estudiantes elaboran un ensayo sobre los siguientes temas¿ Qué es la paz para ti? y¿Cómo crees que se puede conseguir?

• 2. Socialización guiada de la actividad.

SEMANA 10 MATEMÁTICAS

19 AL 23   DE MARZO  

SEMANA SIGUIENTE 26 AL 30 SEMANA SANTA

Repaso de polinomios aritméticos y taller de aplicación.

SEMANA 10 LAS DIFERENTES FORMAS DE RELIEVE

VER EL VÍDEO Y HACER EN EL CUADERNO LAS DIFERENTES FORMAS DEL RELIEVE

SEMANA #9. 2018. EDUCACIÓN ARTÍSTICA Y CULTURAL.

Objetivo: Combinar colores y observar el resultado.

Dibuja en formato horizontal las cuatro frutas entrelazadas, colorea cada una con su color natural, luego traza detrás de ellas una linea horizontal para definir un plano que las soporta, puede ser una mesa, colorea todo el dibujo.

SEMANA # 9 FILOSOFIA

PRUEBA DE PERIODO

•  Repaso
• Presentación de prueba
• Corrección de prueba

SEMANA 9 MATEMÁTICAS

12 AL 16DE MARZO.


SIGNOS DE AGRUPACIÓN Y POLINOMIOS ARITMÉTICOS.

Jerarquía de operaciones.

Hablando de las operaciones básicas (suma, resta, multiplicación y división) éstas observan el siguiente orden:

• Primero se realizan todas las multiplicaciones y divisiones, pues tienen la misma jerarquía. Se realizan siempre de izquierda a derecha. 
• Después se realizan las sumas y restas, igual de izquierda a derecha.

Si se quiere cambiar el orden de operaciones entonces utilizamos signos de agrupación, que son: los paréntesis, los corchetes, y las llaves, también el símbolo de la fracción es un símbolo de agrupación. 

Cuando se tienen varios símbolos, uno dentro de otro, se realizan primero desde adentro hacia afuera. Primero los paréntesis, luego los corchetes y por último las llaves.

Si en el polinomio hay potencias y raíces, se empieza por dichas operaciones.

1.  

Primero se desarrollan las potencias. En este caso es sólo el 5. Hay que observar que se eleva sólo al cuadrado el número sin el signo, pues no está encerrado entre signo de agrupación. El signo no se eleva al cuadrado. Entonces resolviendo, nos queda:

 

Ahora realizamos todas las multiplicaciones y divisiones que encontremos dentro de los símbolos de agrupación, recuerda, de izquierda a derecha. Así que multiplicamos 2*10 y realizamos la división 6/3. Nos queda:

Ahora realizamos las operaciones que están dentro del símbolo de más adentro. -2+2.

y quitamos las llaves

Nuevamente realizamos la operación indicada entre los símbolos de agrupación. -2+0 y nos queda:

Como entre -25 y (-2) no existe algún signo que nos indique operación alguna, significa que es una multiplicación. 

2.

Empezamos por las operaciones indicadas dentro del paréntesis (2-3), la suma de -2-3 y la multiplicación -(-2)

sumamos (2+3) y quitamos el paréntesis

quitamos las llaves del 5 y realizamos la suma resultante.

quitamos las llaves y sumamos

quedando como resultado:

3)    [ 8 + 3 x( 12- 5) ] -7     Se resolvió el parèntesis (12-5)
    = [ 8+ 3 x 7] -7       Se resolvió la multiplicación 3x7
    = [8 + 21 ]-7      Se resuelve la adición 8 + 21
    = 29 - 7       Se resuelve la resta 29-7
    = 22

4)  {[4+( 5 x 8)-2] : 3 } + 11     Resolvemos de adentro hacia afuera:
   =  {[ 4 + 40 -2] : 3 } +11
   = { [4 + 38] : 3} + 11
   = {42 : 3 } + 11
   = 14 + 11
   = 25

TALLER DE APLICACIÓN, SE ENTREGA A CADA ESTUDIANTE EN EL AULA DE CLASE, SE TRABAJA POR PAREJAS.

SEMANA #8. 2018. EDUCACIÓN ARTÍSTICA Y CULTURAL.

Objeto de aprendizaje: Collage de paisaje submarino.

Objetivo:  Desarrollar la capacidad creativa y de composición libre mediante la creación de un collage.
Actividad: Con base a las láminas de especies marinas que trajeron a la clase, crear un collage, complementar con dibujo y color.

La palabra Collage es un término que procede del idioma francés y que ha trasladado una de sus referencias al idioma español, convirtiéndose en un término popular para designar una técnica del arte plástico, que consiste en pegar sobre papel, tela o madera diversos fragmentos de materiales, los cuales tendrán la  finalidad de comunicar un mensaje artístico.

En el ejercicio de hoy los estudiantes trajeron laminas que hacen referencia a animales u objetos encontrados en el fondo marino: peces de diversas especies, barcos hundidos, buzos etc; recortan la silueta, la pegan en hoja de dibujo formato horizontal y posteriormente complementan con dibujo y color la composición.

                                            

Aquí tienes variedad de especies marinas para que complementes tu paisaje submarino, recuerda tu creatividad es primordial en este ejercicio.

SEMANA #7. 2018. EDUCACIÓN ARTÍSTICA Y CULTURAL.

Observaciones: Grado 6°2, asiste a parque explora. Miércoles 28 de febrero de 2018.

Grado 6°1
Objetivo: Desarrollar la imaginación mediante la creación de un dibujo de un castillo fantástico.
Aplicar colores libremente, decorar creativamente.

Objeto de aprendizaje: Dibujo fantástico.
Objetivo: Desarrollar la capacidad de la imaginación con base a una idea.

Imaginación

1.
Facultad humana para representar mentalmente sucesos, historias o imágenes de cosas que no existen en la realidad o que son o fueron reales pero no están presentes.

sinónimos:

fantasía

2.
Capacidad o facilidad para concebir ideas, proyectos o creaciones innovadoras.

1. 
   

Ejercicio de clase: Dibuja un Castillo fantástico,en las nubes.

SEMANA # 8 FILOSOFIA

EMPÉDOCLES TIERRA, AGUA, FUEGO Y AIRE

Empédocles (494- 434 a. de C.) de Sicilia sería el que lograra salir de los enredos enlos que se había metido la filosofía. Opinaba que, tanto

Parménides como Heráclito, tenían razón en una de sus afirmaciones, pero que los dos se equivocaban en una cosa.

Empédocles pensaba que el gran desacuerdo se debía a que los

filósofos habían dado por sentado(error esencial en Parménides)

que había un solo elemento. De ser así, la diferencia entre lo que

dice la razón y lo que «vemos con nuestros propios ojos» seria insuperable.

Es evidente que el agua no puede convertirse en un pez o en una

mariposa. El agua no puede cambiar. El agua pura sigue siendo

agua pura para siempre. De modo que Parménides tenía razón en

decir que «nada cambia».

Al mismo tiempo, Empédocles le daba la razón a Heráclito en que

debemos fiarnos de lo que nos dicen nuestros sentidos. Debemos creer lo que vemos, y vemos, precisamente, cambios constantes en la naturaleza.

Empédocles llegó a la conclusión de que lo que había que

rechazar era la idea de que hay un solo elemento. Ni el agua ni el

aire son capaces, por sí solos, de convertirse en un rosal o en

una mariposa, razón por la cual resulta imposible que la

naturaleza sólo tenga un elemento.

Empédocles pensaba que la naturaleza tiene en total cuatro

elementos o «raíces», como él los llama. Llamó a esas cuatro

raíces tierra, aire, fuego y agua.

Todos los cambios de la naturaleza se deben a que estos cuatro

elementos se mezclan y se vuelven a separar, pues todo está

compuesto de tierra, aire, fuego y agua, pero en distintas

proporciones de mezcla. Cuando muere una flor o un animal, los

cuatro elementos vuelven a separarse. Éste es un cambio que

podemos observar con los ojos. Pero la tierra y el aire, el fuego y

el agua quedan completamente inalterados o intactos con todos

esos cambios en los que participan. Es decir, que no es cierto que

«todo» cambia (en contra de Heráclito). En realidad, no hay nada

que cambie, lo que ocurre es, simplemente, que cuatro elementos

diferentes se mezclan y se separan, para luego volver a

mezclarse.

Podríamos compararlo con un pintor artístico: si tiene sólo un

color –por ejemplo el rojo- no puede pintar árboles verdes. Pero

si tiene amarillo, rojo, azul y negro, puede obtener hasta cientos

de colores, mezclándolos en distintas proporciones.

Un ejemplo de cocina demuestra lo mismo. Si sólo tuviera harina,

tendría que ser un mago para poder hacer un bizcocho. Pero si

tengo huevos y harina, leche y azúcar, entonces puedo hacer un

montón de tartas y bizcochos diferentes, con esas cuatro

materias primas.

No fue por casualidad el que Empédocles pensara que las

«raíces» de la naturaleza tuvieran que ser precisamente tierra,

aire, fuego y agua. Antes que él, otros filósofos habían intentado

mostrar por qué el elemento básico tendría que ser agua, aire o

fuego. Tales y Anaxímenes ya habían señalado el agua y el aire

como elementos importantes de la naturaleza. Los griegos

también pensaban que el fuego era muy importante. Observaban,

por ejemplo, la importancia del sol para todo lo vivo de la

naturaleza, y, evidentemente, conocían el calor del cuerpo

humano y animal.

Quizás Empédocles vio cómo ardía un trozo de madera; lo que

sucede entonces, es que algo se disuelve. Oímos cómo la madera

cruje y gorgotea. Es el agua. Algo se convierte en humo. Es el

aire. Vemos ese aire. Algo queda cuando el fuego se apaga. Es la

ceniza, o la tierra.

Empédocles señala, como hemos visto, que los cambios en la

naturaleza se deben a que las cuatro raíces se mezclan y se

vuelven a separar. Pero queda algo por explicar. ¿Cuál es la causa

por la que los elementos se unen para dar lugar a una nueva

vida? ¿Y por qué vuelve a disolverse «la mezcla», por ejemplo,

una flor?

Empédocles pensaba que tenía que haber dos fuerzas que

actuasen en la naturaleza. Las llamó «amor» y «odio». Lo que une

las cosas es «el amor», y lo que las separa, es «el odio».

Tomemos nota de que el filósofo distingue aquí entre

«elemento» y «fuerza». Incluso, hoy en día, la ciencia distingue

entre «los elementos» y «las fuerzas de la naturaleza». La ciencia

moderna dice que todos los procesos de la naturaleza pueden

explicarse como una interacción de los distintos elementos, y

unas cuantas fuerzas de la naturaleza.

Empédocles también estudió la cuestión de qué es lo que pasa

cuando observamos algo con nuestros sentidos. ¿Cómo puedo

ver una flor, por ejemplo? ¿Qué sucede entonces? ¿Has pensado

en eso, Sofía? ¡Si no, ahora tienes la ocasión!

Empédocles pensaba que nuestros ojos estaban formados de

tierra, aire, fuego y agua, como todo lo demás en la naturaleza. Y

«la tierra» que tengo en mi ojo capta lo que hay de tierra en lo

que veo, «el aire» capta lo que es

 de aire, «el fuego» de los ojos

capta lo que es de fuego y «el agua» lo que es de agua. Si el ojo

hubiera carecido de uno de los cuatro elementos, yo tampoco

hubiera podido ver la naturaleza en su totalidad.

TALLER

1. ¿ En qué les da la razón y en qué se las quita Empédocles, a Heráclito y Parménides?

2. ¿Por qué Empédocles rechaza la idea de que hay un sólo elemento de donde se origina todo?

3. ¿Cuáles son los elementos o raíces, que Empédocles considera como originarios de todo?

4. Interpreta la teoría de Empédocles a través del ejemplo de la elaboración de un bizcocho.

5. ¿Cuál es la causa por la que los elementos de Empédocles se unen y se separan?

6. ¿Estás de acuerdo con la teoría de Empédocles? ¿ Por qué?

7. Socialización y análisis del taller

SEMANA 8 MATEMÁTICAS

5 AL 9 DE MARZO

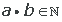
Multiplicar dos números naturales consiste en sumar uno de los factores consigo mismo tantas veces como indica el otro factor.

Por ejemplo, la multiplicación 2·5 consiste en sumar el número 2 cinco veces:

2·5 = 2 + 2 + 2 + 2 + 2 = 10

Términos que intervienen en una multiplicación:

     a · b = c

 a y b se denominan factores

 El resultado (c) se denomina producto

Propiedades de la multiplicación de números naturales

1 CLAUSURATIVA

El resultado de multiplicar dos números naturaleses otro número natural.

     

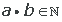
2 Asociativa

El modo de agrupar los factores no varía el resultado.

     (a · b) · c = a · (b · c)

Ejemplo:

(2 · 3) · 5 = 2 · (3 · 5)
6 · 5 = 2 · 15
30 = 30

3 Conmutativa

El orden de los factores no varía el producto.

     a · b = b · a

Ejemplo:

2 · 5 = 5 · 2
10 = 10

4 Elemento neutro

El 1 es el elemento neutro de la multiplicación de números naturales porque todo número multiplicado por él da el mismo número.

     a · 1 = 1 · a = a

Ejemplo:

3 · 1 = 1 · 3 = 3

5 Distributiva

La multiplicación de un número natural por una suma es igual a la suma de las multiplicaciones de dicho número natural por cada uno de los sumandos.

     a · (b + c) = a · b + a · c 

Ejemplo:

2 · (3 + 5) = 2 · 3 + 2 · 5
2 · 8 = 6 + 10
16 = 16

SE REALIZA TALLER DE APLICACIÓN QUE SE ENTREGA EN EL AULA.