SEMANA 20 MATEMÁTICAS EMILSE

4 AL 8 DE JUNIO

APLICACIÓN DEL EXÁMEN TIPO ICFES DE FINAL DE PERÍODO


DESCOMPOSICIÓN DE UN NÚMERO EN FACTORES PRIMOS

Todo número compuesto se puede escribir como multiplicación de dos o más factores primos.

Para descomponer un número en producto de factores primos se siguen estos pasos:

1° Se escribe el número a la izquierda de una raya vertical (actúa como "ventana" de división) y a su derecha el menor número primo (2, 3, 5, 7,... ) por el cual dicho número sea divisible. El cociente obtenido se coloca debajo del número propuesto. 

2° Se procede como en el paso anterior con el cociente obtenido, y así sucesivamente hasta llegar a un cociente igual a 1.

Ejemplo 1:  Realiza la descomposición en producto de factores primos del número 24:

Los números que están a la izquierda de la línea, son los cocientes parciales y los de la derecha, son los factores primos.

Recuerda que siempre debes comenzar por el menor número primo por el cual, el número que te están preguntando, sea divisible.

Ejemplo 2:  Realiza la descomposición en producto de factores primos del número 60:

Ejemplo 3:  Realiza la descomposición en producto de factores primos del número 180:

Debes recordar :

- Números primos: Un número natural distinto de 1 es número primo si solo tiene como divisores la unidad y el mismo número. Ejemplo:  2, 3, 5, 7, 11. 13, 17, 19, 23, 29, ...

- Números compuestos: Un número natural es compuesto si tiene otros divisores además del 1 y del mismo número. Ejemplo: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20,...

- Factor: Es un número que se multiplica por otro para hallar un producto.

- Factores comunes: son factores de dos o más números.

MEDIDAS DE LONGITUD

La longitud determina la distancia que hay entre dos puntos, o dicho de otra manera, longitud es la cantidad de espacio que hay entre dos puntos. Por ejemplo, la distancia que hay entre mi casa y el colegio, o la distancia de un extremo de la mesa al otro.

La unidad principal para medir la longitud es el metro. Por ejemplo, un metro es lo que mide de largo una guitarra.

1 metro

 

Pero, ¿qué hago si quiero medir objetos mucho más pequeños? ¿U objetos mucho más grandes?

Para eso tenemos más medidas de longitud: los múltiplos y los submúltiplos del metro.

• Los múltiplos son las unidades de medida más grandes que el metro. Son el decámetro, el hectómetro y el kilómetro. Hay más pero de momento solo vamos a ver estas.
• Los submúltiplos son las unidades de medida más pequeñas que el metro. Son el decímetro, el centímetro y el milímetro.

En la siguiente tabla se muestran las medidas de longitud:

Para que tengas una idea aproximada de las distancias que miden los múltiplos y los submúltiplos vamos a ver los siguientes ejemplos:

La distancia entre Málaga y Santander es de aproximadamente 900 kilómetros.

La longitud de un campo de fútbol es de aproximadamente 1 hectómetro.

La longitud de un autobús es de aproximadamente 1 decámetro.

La altura de una botella de agua es de aproximadamente 2 decímetros.

La longitud de una pelota de tenis es de aproximadamente 6 centímetros.

Para convertir las unidades de longitud, es importante conocer su simbología y equivalencias:

km = kilómetro

hm = hectómetro

dam = decámetro

m = metro

dm = decímetro

cm = centímetro

mm = milímetro

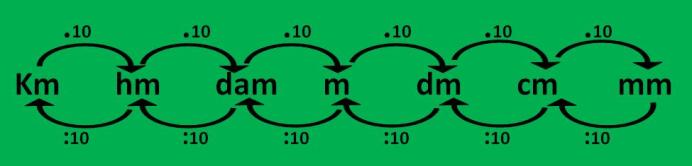
Ahora, observa el siguiente gráfico:

Además debes saber :

*Las unidades mayores se ubican hacia la izquierda y las unidades menores, a la derecha. Por tanto,  si quiero convertir m a km, estaría convirtiendo una unidad menor a una unidad mayor, también si convierto  mm a dm, estaría convirtiendo una unidad menor a otra mayor. Por el contrario, si convierto  km a dam, estaría convirtiendo una unidad mayor a otra menor, también, si convierto  m a mm, estaría convirtiendo una unidad mayor a otra menor.

Conozcamos algunas  equivalencias:

1 m = 10 dm                   1 km  = 1000 m

1 m = 100 cm                 1 hm =    100 m

1 m = 1000 mm             1 dam =   10 m

Procedimiento para convertir unidades de longitud:

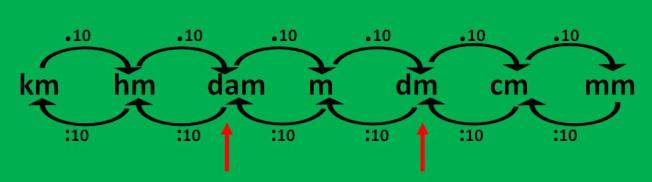
1.Ubica la unidad que vas a convertir y  la unidad convertida en el gráfico:

Convertir  23 m a  mm

Cuando conviertes 23 m a mm, estás convirtiendo una unidad mayor  a otra menor, observa que el único camino que podemos usar son las flechas de arriba, estas me indican que se multiplica .10 .10 .10  esto es igual a 1000.

2. Por tanto 23 m a mm será: 23.1000 =  23000 mm

3. Podemos concluir, que cuando convertimos una unidad mayor a otra menor, se multiplica.

OTRO EJEMPLO:

Convertir 28000 dm a dam

1. Ubica la unidad que vas a convertir y la unidad convertida en el gráfico:

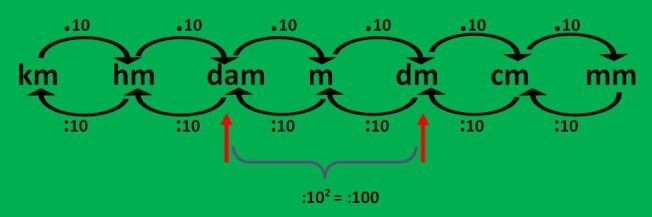
Cuando conviertes 28000 dm a dam, estás convirtiendo una unidad menor  a otra mayor, observa que el único camino que podemos usar son las flechas de abajo, estas me indican que se divide :10 :10  esto es igual a :100

2. Por tanto 28000 dm a dam será: 28000:100 =  280 dam

3. Podemos concluir, que cuando convertimos una unidad menor a otra mayor, se divide.

ALGUNOS EJERCICIOS:

1. Convierte a la unidad indicada entre paréntesis:

Ejemplo:

56 dm (mm)

56. 100 = 5600 mm

a. 240000 m (km)

b. 36 dm (mm)

c. 78000 mm (m)

2. Convierte a la mayor unidad de medida posible sin usar la coma decimal

Ejemplo:

23000 m

23000 : 1000 = 23 km

a. 57000 cm

b. 3600 m

c. 4900000 mm

3. Escribe la unidad mayor y la unidad menor siguiente :

Unidad mayor siguiente		Unidad menor siguiente
23 dm	230 cm	2300 mm
	5600 dm
	670 m
	45500 hm

4. Calcula:

Ejemplo:

27 m  + 12 km =  27 m + 12000m = 12027 m

a. 78 mm + 34dm =

b.56 m + 34 cm =

c.27 dm – 120 cm =