SEMANA DIEZ MATEMÁTICAS

20 al 24 de marzo

Exámen final del período  y autoevaluación.

MÚLTIPLOS DE UN NÚMERO

Un número a es múltiplo de otro b cuando es el resultado de multiplicar este último por otro número c.


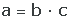
Dado un número natural obtenemos un múltiplo de él al multiplicarlo por otro número natural.
Ejemplo:


18 = 2 · 9 18 es múltiplo de 2, ya que resulta de multiplicar 2 por 9.

Tabla de múltiplos de los números:

Múltiplos del número 2
2 · 0 = 0

2 · 1 = 2 

2 · 2 = 4 

2 · 3 = 6 

2 · 4 = 8
2 · 5 = 10 

2 · 6 = 12 

2 · 7 = 14 

2 · 8 = 16 

2 · 9 = 18

Múltiplos del número 3
3 · 0 = 0

3 · 1 = 3 3

 · 2 = 6 

3 · 3 = 9 

3 · 4 = 12
3 · 5 = 15 

3 · 6 = 18 

3 · 7 = 21 

3 · 8 = 24

 3 · 9 = 27

Múltiplos del número 4
4 · 0 = 0

4 · 1 = 4 

4 · 2 = 8 

4 · 3 = 12 

4 · 4 = 16
4 · 5 = 20 

4 · 6 = 24 

4 · 7 = 28 

4 · 8 = 32 

4 · 9 = 36

Múltiplos del número 5
5 · 0 = 0 5

 · 1 = 5 

5 · 2 = 10 

5 · 3 = 15 

5 · 4 = 20

5 · 5 = 25 

5 · 6 = 30 

5 · 7 = 35 

5 · 8 = 40 

5 · 9 = 45

Múltiplos del número 6
6 · 0 = 0

 6 · 1 = 6 

6· 2 = 12 

6 · 3 = 18 

6 · 4 = 24
6 · 5 = 30 

6 · 6 = 36 

6 · 7 = 42 

6 · 8 = 48 

6 · 9 = 54


Múltiplos del número 7
7 · 0 = 0           7 · 1 = 7         7 · 2 = 14       7 · 3 = 21        7 · 4 = 28
7 · 5 = 35         7 · 6 = 42        7 · 7 = 49       7 · 8 = 56       7 · 9 = 63

Múltiplos del número 8
8 · 0 = 0

8 · 1 = 8 

8 · 2 = 16

 8 · 3 = 24

 8 · 4 = 32
8 · 5 = 40 

 8 · 6 = 48 

8 · 7 = 56

 8 · 8 = 64 

8 · 9 = 72

Múltiplos del número 9
9 · 0 = 0 

9 · 1 = 9 

9 · 2 = 18 

9 · 3 = 27 

9 · 4 = 36
9 · 5 = 45 

9 · 6 = 54 

9 · 7 = 63 

9 · 8 = 72 

9 · 9 = 81

Múltiplos del número 10
10 · 0 = 0 

10 · 1 = 10 

10 · 2 = 20 

10 · 3 = 30 

10 · 4 = 40
10 · 5 = 50 

10 · 6 = 60 

10 · 7 = 70 

10 · 8 = 80 

10 · 9 = 90

DIVISORES DE UN NÚMERO
Un número b es un divisor de otro a cuando lo divide exactamente.
A los divisores también se les llama factores.
Ejemplo:


12 : 4 = 3  4 es divisor de 12

4 · 3 = 12  12 es múltiplo de 4

Criterios de divisibilidad

Un número b es divisible por otro a cuando la división es exacta.

Criterio de divisibilidad por 2
Un número es divisible por 2, si termina en cero o cifra par.
Ejemplo:
24, 238, 1 024, ...

Criterio de divisibilidad por 3

Un número es divisible por 3, si la suma de sus dígitos es múltiplo de 3.
Ejemplo:


564  5 + 6 + 4 = 15 15 es múltiplo de 3

2 040 2 + 0 + 4 + 0 = 6  6 es múltiplo de 3
Criterio de divisibilidad por 5
Un número es divisible por 5, si termina en cero o cinco.
Ejemplo:
45, 515, 7 525, 230, ...

Criterio de divisibilidad por 7
Un número es divisible por 7 cuando la diferencia entre el número sin la cifra de las unidades y el doble de la cifra de las unidades es 0 ó un múltiplo de 7.
Ejemplo:


343  34 − 2 · 3 = 28 28 es múltiplo de 7

105  10 − 5 · 2 = 0

2 261  226 − 1 · 2 = 224
Se repite el proceso con 224 22 − 4 · 2 = 14 14 es múltiplo de 7

Criterio de divisibilidad por 11
Un número es divisible por 11, si la diferencia entre la suma de las cifras que ocupan los lugares impares y la de los pares es 0 o un múltiplo de 11.
Ejemplo:


121 (1 + 1) − 2 = 0

4224 (4 + 2) − (2 + 4) = 0


Otros criterios de divisibilidad

Criterio de divisibilidad por 4
Un número es divisible por 4, si sus dos últimas cifras son ceros o múltiplo de 4.
Ejemplo:
36, 400, 1 028, ...

Criterio de divisibilidad por 6
Un número es divisible por 6, si es divisible por 2 y por 3.
Ejemplo:
72, 324, 2 400, ...

Criterio de divisibilidad por 8
Un número es divisible por 8, si sus tres últimas cifras son ceros o múltiplo de 8.
Ejemplo:
4 000, 1 048, 1 512, ...

Criterio de divisibilidad por 9
Un número es divisible por 9, si la suma de sus dígitos es múltiplo de 9.
Ejemplo:


81 8 + 1 = 9

3 663 3 + 6 + 6 + 3 = 18  18 es múltiplo de 9

Criterio de divisibilidad por 10

Un número es divisible por 10, si la cifra de las unidades es 0.
Ejemplo:
130, 1 440, 10 230, ...

TALLER Nº----------

1. Resolución de ejercicios buscando múltiplos y divisores de un número, encontrando números primos y compuestos.

2. Solucionar ejercicios aplicando todos los criterios de divisibilidad de un número a números dados.

Se entrega la copia del taller en el aula de clase.