SEMANA 5 RELIGION

SEMANA 5 RELIGIÓN 13 -02 -17

LA PERSONA - GRADO SEXTO

LA HISTORIA DE MI VIDA

Conducta de entrada:
a. ¿Qué momentos de tu historia de vida han sido más importantes?
b. ¿Quienes han ayudado a construir tu historia de vida?
c. ¿Cómo crees que será tu historia de vida en los próximos 10 años?

Todos los seres humanos tenemos una historia personal. Nuestra historia comenzó al momento de nacer y se ha venido desarrollando a través de los momentos cotidianos e importantes de nuestra vida. Algunos ya conocen en parte la historia de sus compañeros porque desde hace algún tiempo estudian juntos. De otros, no saben nada, porque apenas comienzan a construir historia juntos, al ser ahora compañeros de curso. Unos y otros, al compartir ahora su historia de vida están llamados a ser amigos.

En la historia de cada uno hay momentos importantes por lo que han significado para nosotros. El momento más importante de nuestra vida es cuando elegimos lo que queremos Ser y Hacer con nuestras vidas, ya que en esa elección expresamos el modo como queremos realizarnos como personas. Algunos, ya habrán pensado qué quieren ser cuando acaben bachillerato; otros quizás aún no lo han pensado. Unos, habrán pensado en casarse y tener hijos; otros, en seguir solteros. Aunque no tengamos claro aún lo que queremos ser y hacer cuando seamos adultos, el comenzar a pensar desde ya en ello, nos ayuda a descubrir el modo como queremos realizarnos, ser felices y dejar huella en este mundo.

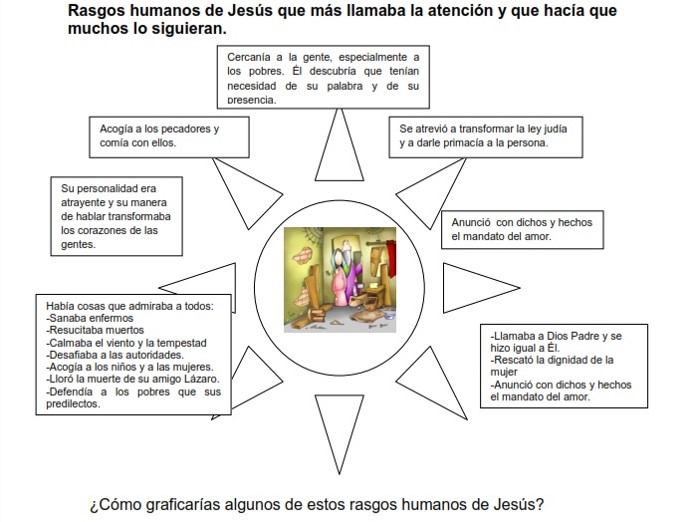
Sabias que... Para los cristianos, la Biblia es el libro que narra la historia de la vida de alguien importante para ellos. En ella se encuentra la historia de la vida de Jesús y de sus discípulos. Especialmente en los cuatro Evangelios encontramos los momentos importantes de la vida de Jesús y sus discípulos y el sentido que ellos les dieron a los mismos.

ACTIVIDAD

1. Buscar en la Biblia, los siguientes textos bíblicos y analizar sobre los momentos de la vida de Jesús:
Lucas 1, 26-38; 2, 1-5; 3, 21-37; 23, 44-49; 24, 1-12

2. Realizar con la ayuda de tus padres la historia de tu vida identificando algunos momentos importantes y significativos en forma de cuento, historieta, ayudado de dibujos, recortes y/o fotos.

SEMANA 11 RELIGION

SEMANA  23 / 03/  17


Realizar una  sopa de letras con las  siguientes palabras:











.

SEMANA 19 RELIGION

SEMANA 30 /  05/  17


         ¿De dónde nace la dignidad del hombre?

La dignidad del hombre nace de ser creado por Dios a su imagen y semejanza, de haber sido reconciliado por Cristo y de estar llamado, mediante la gracia, a alcanzar su plenitud en la bienaventuranza del cielo.

¿Cómo puede el hombre llegar a la felicidad del cielo?

Mediante el ejercicio de su libertad, practicando el bien, cumpliendo en su vida el amoroso plan que Dios tiene para él.

¿Qué es la libertad?

La libertad es la capacidad que tiene el hombre de ejecutar por sí mismo acciones deliberadas. La libertad es en el hombre signo eminente de la imagen divina.

¿Cuándo la libertad humana alcanza su grado máximo?

La libertad humana alcanza su grado máximo cuando el hombre descubre el pan de amor que Dios tiene para él y lo vive plenamente en su actuación diaria.

   

SEMANA 19 EVALUACIÓN DE PERIODO

Repasr todos los conceptos vistos en este periodo para la evaluación

SEMANA 19

29 AL 2 DE JUNIO

29 AL 2 DE JUNIO
29-------FESTIVO
30---31----1----CESE DE ACTIVIDADES


VIERNES 2 DE JUNIO-----REINGRESO----


Multiplicar números decimales por 10, 100, 1000…

Para multiplicar un número decimal por 10, 100, 1000… lo único que tendremos que hacer es mover la coma del decimal a la derecha tantas posiciones como ceros tenga el número.

Por ejemplo:

Como el 100 tiene dos ceros moveremos la coma dos posiciones a la derecha. Por lo tanto, el resultado es 315,4

Dividir números decimales por 10, 100, 1000…

Para dividir un número decimal por 10, 100, 1000… lo único que tendremos que hacer es mover la coma del decimal a la izquierda tantas posiciones como ceros tenga el número.

Por ejemplo:



Como el 10 tiene un cero moveremos la coma una posición a la izquierda. Por lo tanto, el resultado queda 8,42

Multiplicaciones por 10, 100, 1 000...20, 200, 2 000...

Una multiplicación por múltiplo de 10 (10, 100, 1 000...) puede realizarse mentalmente, porque basta con agregar al número del primer factor tantos ceros como tiene el múltiplo de 10 por el que se está multiplicando.

Ejemplos:

Multiplicaciones por 10, 100, 1 000...

Una multiplicación por múltiplo de 10 (10, 100, 1 000...) puede realizarse mentalmente, porque basta con agregar al número del primer factor tantos ceros como tiene el múltiplo de 10 por el que se está multiplicando.

Ejemplos:



Una multiplicación por un múltiplo de 10 (20, 200, 2 000...30, 300, 3 000, 40, 400, 4 000...) podemos realizarla multiplicando el número sin los ceros y luego agregamos tantos ceros como los que tenga el múltiplo de 10.


Ejemplos:

TALLER JUNIO 2

MULTIPLICAR POR 10 , 100 ,1.000 

1.¿Qué hay que hacer para multiplicar un número por 10?Pon un ejemplo

2. Pon un ejemplo. ¿Cómo multiplicamos un número por 100? 

3 Multiplica por 10 las siguientes cantidades: 

• 42 x 10 =
•  12.365 X 100000= 
• 57 x 1000 = 
• 698 X 100= 
• 15976 x 100 = 12 X 100000= 
• 23289 x 1000 =
•  53675 X 10= 

4.. Multiplica estos números por 100: 

• 12x 100 = 70
• 345,9458 x 100 = 
• 47,368 X 100= 
• 129,57 x 100 = 
• 2,5 X 100= 
• 9,8 X 100= 
• 6,9676 x 100 = 
• 1,286 X 100= 
• 4,91264 X 100= 
• 0,234 X 100
• X 100
• 0,68 X 100

5. Divide estas cantidades por 1.000: 

• 3 : 1000 = 
• 13,6 : 1000=
•  7 : 1000 = 
• 9,784 : 1000= 
• 12 : 1000 = 
• 196,5 : 1000= 
• 298,97 : 1000 =
• 69,8 : 1000= 
• 0,34 : 100
• 0,0004156:100
• 07 :1000
• 0,254 :10000

Semana 18: Flujo de la materia y la energia

Propósito:
Explicar como circula la materia y la energía en los ecosistemas 

                                                                            Redes tróficas

Una red trófica nos indica la forma como la energía química de los organismos se va pasando de un organismo a otro a través de cadenas alimenticia; en la naturaleza esto se entiende como una pirámide con varios niveles concretos donde  cada uno, sería un eslabón diferente de la cadena alimenticia y recibe el nombre de nivel trófico; las plantas forman el primer escalón donde la base de la pirámide aportan la energía al resto de los seres vivos y el escalón siguiente está formado por consumidores primarios, es decir, la mayoría de animales, en el siguiente nivel están los animales que se alimentan de otros animales de manera directa o indirecta y  a medida que se asciende por la pirámide también crece el tamaño de los individuos.

Que debes hacer.

1.  Elabora una síntesis del audiovisual. 
2. Elabora el glosario con las palabras utilizadas en el audiovisual. 
3. Dibuja en tu cuaderno una red trófica con los organismos que conoces en tu región.  
4. Explica porque es importante las redes tróficas en los ecosistemas. 

SEMANA #18. EDUCACIÓN ARTÍSTICA Y CULTURAL

Actividad #1.  Tema: El respeto

Objetivo: Promover el desarrollo de la escritura, de forma estética, legible y con buena ortografía; a partir de frases formativas  que contribuyan a la activación del pensamiento  crítico reflexivo y a la comprensión lectora.

Ejercicio:En el cuaderno de Caligrafía: escribir la frase y realizar la reflexión personal.

Actividad #2.  Tema: Pixel-art

Objetivo: conocer y practicar la técnica artística pixel-art.

Ejercicio de clase: los estudiantes del grado 6°1, continúan trabajando el dibujo.

Con base a la técnica trabajada a partir de las hojas cuadrículadas, realizar un diseño pixelado.

Sigue la cuadrícula  y verás que es fácil hacerlo.  Suerte!

Aquí tienes unas muestras, puedes crear los tuyos si prefieres o buscar otras ideas.

SEMANA 16 RELIGION

SEMANA  08 / 05 /  17

La dignidad humana es el derecho que tiene cada ser humano, de ser respetado y 

valorado como ser individual y social, con sus características y condiciones particulares,

 por el solo hecho de ser persona. La historia nos muestra muchos casos en que

 la dignidad humana ha sido avasallada.

      

La dignidad del hombre nace del hecho de haber sido creado por Dios a su imagen y semejanza, haber sido reconciliado por Cristo y estar llamado a la Bienaventuranza del Cielo.

Es tanta la dignidad del hombre, que el Concilio Vaticano II afirma que el hombre es la "única criatura en la tierra a la que Dios ha amado por sí misma" (Gaudium et Spes, 24,3).

El hombre, ayudado por la gracia y usando bien de su libertad, puede identificar su voluntad con la voluntad de Dios, pues "Lo que Dios quiere es siempre lo óptimo" 

SEMANA 18 RELIGION

SEMANA 22 /  05/  17


ACTIVIDAD

Buscar en la biblia algunos de los rasgos humanos de Jesús




 Ejemplos de los rasgos humanos de Jesús : Mateo 19:14

                 

               

SEMANA 17 RELIGION

SEMANA 15 / 05 / 17

1

    
                        
  

SEMANA 18 EL HOMO SAPIENS SAPIENS

VER el video y dibujar y describir este momento de la evolución del ser humano

SEMANA 18

22 AL 25 DE MAYO

CESE DE ACTIVIDADES

SEMANA #17. EDUCACIÓN ARTÍSTICA Y CULTURAL.

Observación: debido a la anormalidad académica los estudiantes no asisten al colegio, sin embargo deben trabajar la actividad en la casa.

Con base a la técnica trabajada a partir de las hojas cuadrículadas, realizar un diseño pixelado.
Sigue la cuadrícula  y verás que es fácil hacerlo.  Suerte!

Aquí tienes unas muestras, puedes crear los tuyos si prefieres o buscar otras ideas.

SEMANA 17 EL AUSTRALOPHITECUS

Ver el video y escribir las características de este momento d ela evolución del hombre

DIA DEL CINE

SEMANA #16. EDUCACIÓN ARTÍSTICA Y CULTURAL.

Tema: el respeto
En el bloc, tipo afiche

Objetivo: Promover el desarrollo de la escritura, de forma estética, legible, con buena ortografía; a partir de frases  que contribuyan a la activación del pensamiento  crítico reflexivo y a la comprensión lectora.

Ejercicio: escribir la frase y la reflexión personal sobre la practica del respeto en el colegio

                                                Actividad #2.  En el bloc de artística

Diseños Geométricos con base a hojas cuadrículadas.

Observación ADIDA convoca a paro por tal motivo se aplaza la actividad.
Los estudiantes que quieran pueden trabajar la frase en el bloc y terminar el diseño con base a hojas cuadrículas

SEMANA 16 LA EVOLUCIÓN DEL HOMBRE

Dibujar los diferentes momentos de la evolución del hombre y describir sus características

SEMANA # 16 FILOSOFIA

SENTIDOS O RAZÓN… ESE ES EL DILEMA

TITULO: ¿Sentidos o razón?… ese es el dilema

TEMA: el racionalismo y el empirismo

PROPÓSITO: re- contextualizar a los estudiantes frente a lo que podríamos llamar los primeros filósofos racionalistas y empiristas. Platón y Aristóteles.

ACTIVIDADES protocolo de la clase anterior, análisis de aforismo, Sopa de letras individual con vocabulario del tema?, taller grupal, socialización con debate, vídeo, tarea.

RECURSOS: Computador, copias del taller.

ü  RECORDEMOS: Antes de comenzar los acuerdos d clase:

• Escucha del otro
• Respeto por la opinión del otro independientemente de que esté de acuerdo o en desacuerdo con su posición
• Para vivir una sana  convivencia en el aula de clase

ü  PROTOCOLO DE LA CLASE ANTERIOR

1. Hermenéutica de los siguientes aforismos por los estudiantes:

 “Un hombre que no arriesga nada por sus ideas, o no valen nada sus ideas, o no vale nada el hombre”.Platón

“Nada hay en el entendimiento que antes no haya pasado por los sentidos” Aristóteles.

2. Pido a los estudiantes que me recuerden lo que vimos la clase pasada sobre lo que es el origen del conocimiento. Frente a la pregunta cuál es el origen del conocimiento que respuestas recuerdan que hubo. Para llegar al racionalismo y el empirismo.

3. Sopa de letras

4. taller grupal sobre la teoría del mundo de las ideas de Platón y teoría de Aristóteles.

5. debate entre aristotélicos y platónicos, con preguntas concretas dirigidas por la docente. Ahí se puede sacar la manzana y preguntar  cómo me explican si la idea de esta manzana en mi mente se obtuvo primero por los sentidos o hubo una idea. Anterior y después de una conclusión. Se pregunta y frente a una casa que fue primero la casa o la idea.( para que ellos construyan sus propios conocimientos.

6. Vídeo

7. Pregunta sobre los conocimientos adquiridos durante la clase.

8 trabajo en colaboración con los padres de familia. Cuéntale a tus padres o a uno de ellos sino es posible a los dos con ejemplos sencillos qué cómo se adquiere el conocimiento a través de los sentidos o a través de la razón. y pregúntales si la enseñanza de los valores que les trasmiten a sus hijos es  sobre ser padres  por la experiencia o por la razón y por qué

SEMANA 17

5 al 9 de junio

 Puedes jugar a construir o medir ángulos, haciendo click en los siguientes enlaces:
Ver enlace:
http://es.wikihow.com/usar-un-transportador
VER ENLACE CÓMO CONSTRUIR ÁNGULOS
AQUÍhttps://www.geogebra.org/m/KWgjwbbA

VER ENLACE CÓMO MEDIR ÁNGULOS
AQUÍhttps://www.geogebra.org/m/KWgjwbbA

 Ángulos

Se toma un punto del plano y partiendo de ese punto, se dibujan dos semirrectas. A la abertura formada por las dos semirrectas se le llama ángulo.

Definición de ángulo

Se llama ángulo a la parte del plano delimitada por dos semirrectas que parten de un mismo punto llamado vértice. A cada semirrecta se le llama lado del ángulo.

- Los lados del ángulo son las semirrectas que lo forman.

- El vértice del ángulo es el punto común que es origen de los lados.

Los tipos de ángulos son:

Agudo < 90°-------Su abertura mide menos que 90º.
Recto = 90º--------Su abertura mide igual a 90º.
Obtuso > 90°-------Su abertura mide más que 90º.
Convexo < 180°-------Su abertura mide  más de 0º y menos de 180º.
Llano = 180°-------Su abertura mide exactamente 180º.
Cóncavo > 180°------Su abertura mide más de 180º y menos de 360º.
Completo = 360°------es un ángulo que mide 360º. Se llama de giro completo.
Nulo = mide 0º

 

2- Tipos de ángulos según su medida
 

Agudo < 90°	Recto = 90°	Obtuso>90°

 

 Ángulos rectos
Un ángulo recto es un ángulo que mide exactamente 90°. Si te das cuenta, en la esquina del ángulo hay un símbolo especial, una caja. Si ves ese símbolo, el ángulo es recto. No se suele escribir el 90°. Si ves la caja en la esquina ya te están diciendo que es un ángulo recto.

Un ángulo recto puede estar en cualquier orientación o giro, lo que importa es que el ángulo interior sea 90°

 Ángulos agudos
Un ángulo agudo es un ángulo que mide menos de 90°. 

Acuérdate de fijarte en cuál de los dos ángulos es al que se refiere uno. Si el ángulo pequeño es menor que 90°, entonces ese es agudo.

Ángulos obtusos
Un ángulo obtuso es un ángulo que mide más de 90° pero menos de 180°. 

 

Acuérdate de fijarte en cuál de las dos partes es a la que se refiere uno. El ángulo más pequeño entre las líneas es obtuso si mide entre 90° y 180°.
 

 Algunas cosas importantes que debes saber

Los ángulos que miden 180° se denominan ángulos extendidos o llanos.

Ángulos cóncavos:Los ángulos que miden más de 180° y menos de 360° se denominan ángulos cóncavos.

Los ángulos que miden 360° se denominan ángulos completos.

El ángulo nulo está formado por dos semirrectas coincidentes, por lo que su abertura es nula, es decir, 0°.
 

 

Los ángulos pueden nombrarse utilizando letras griegas. Por ejemplo:

 

 

 Cómo medir ángulos usando el transportador

Medir un ángulo significa determinar su amplitud y, para hacerlo generalmente se utiliza el transportador.

Un transportador es un instrumento en forma circular o semicircular y graduado angularmente.

Los ángulos se miden en grados sexagesimales. Un grado corresponde a la medida del ángulo que se forma cuando una circunferencia se divide en 360 partes iguales.

Los grados indican la separación delos lados del ángulo. Mientras más separados están los rayos que forman el ángulo, mayor es la cantidad de grados que este mide.

 Para medir ángulos utilizando el transportador semicircular debes:

1° Colocar el trazo recto del transportador sobre uno de los lados del ángulo.

2° Hacer que el punto medio de ese trazo coincida con el vértice del ángulo.

3° Observar el otro lado del ángulo y su valor según la escala angular del transportador. Si el ángulo está abierto hacia la izquierda debes  fijarte en la escala externa y si está abierto hacia la derecha en la escala interna.

 Para medir ángulos utilizando el transportador circular debes:

1° Colocar uno de los lados del ángulo frente al 0°.

2° Hacer coincidir el centro de la circunferencia con el vértice del ángulo.

3° Observar el otro lado del ángulo y su valor según la escala angular del transportador.

SEMANA 16

8 AL 12 DE MAYO

POLÍGONOS CÓNCAVOS Y CONVEXOS

Polígonos

Un polígono es una figura plana con lados rectos.

¿Es un polígono?

Los polígonos son formas bidimensionales. Están hechos con líneas rectas, y su forma es "cerrada" (todas las líneas están conectadas).

Polígono (lados rectos)	No es un polígono (tiene una curva)	No es un polígono (abierto, no cerrado)

Cóncavo o convexo

 Un polígono convexo no tiene ángulos que apunten hacia dentro. Enconcreto, los ángulos internos no son mayores que 180°.Ejemplo:

Definición de Polígono Cóncavo: 

Polígono Cóncavo

Los Polígonos Cóncavos son Polígonos en los que:

1. alguno de sus ángulos internos mide más de 180º 
2. alguna de sus diagonales es exterior.

El polígono de la figura de la izquierda es cóncavo porque el ángulo interior del vértice B tiene más de 180º y además  existe una diagonal externa que no pasa por el interior del polígono como la diagonal. 

Si hay algún ángulo interno mayor que 180° entonces es cóncavo. (Para acordarte: cóncavo es como tener una "cueva")

Convexo	Cóncavo

Regular o irregular

Si todos los ángulos son iguales y los lados también, es regular, si no es irregular

Regular	Irregular

Un polígono regular es el que tiene sus ángulos iguales y sus lados iguales.

Elementos de un polígono regular

1. Centro: Punto interior que equidista de cada vértice.

2. Radio: Es el segmento que va del centro a cada vértice.

3. Apotema: Distancia del centro al punto medio de un lado.

Más ejemplos

Polígono complejo (un "polígono estrellado", en este caso un pentagrama)	Octágono cóncavo	Hexágono irregular

Máximo común divisor

Los divisores de un número son aquellos que al dividir el número el resto es 0.

Por ejemplo: Divisores de 24 son: 1, 2, 3, 4, 6, 12 y 24.

Si se divide 24 por cualquiera de ellos el resto es 0.

El Máximo Común Divisor (M.C.D.) de 2 o más número es el mayor de los divisores comunes a estos números:

Por ejemplo: vamos a calcular el MCD de 30 y 42:

Divisores de 30: 1, 2, 3, 5, 6, 10, 15 y 30.

Divisores de 42: 1, 2, 3, 6, 7, 21 y 42.

Vemos que 6 es un divisor común a ambos números y es el mayor de los divisores comunes. Por lo tanto 6 es el Máximo Común Divisor.

Método abreviado para el m.c.m.

Se divide cada uno de los números dados por su menor divisor; lo mismo se hace con los cocientes hasta obtener que todos los cocientes sean 1. El mcm sera el producto de todos los divisores primos.

Si un número no es divisible por un factor primo se repite debajo (se baja) como sigue en los ejemplos siguientes.

Hallar el m.c.m. de 30, 60 y 190.

Se presinde del 30 porque es divisor del 60.

60	190	2
30	95	2
15	95	3
5	95	5
1	19	19
	1

m.c.m. = 2x2x3x5x19=1140.

Como pueden observar el número 95 no era divisible ni por el factor primo 2 ni por el 3 así que se bajo hasta que se pudo dividir por el factor primo 5.


MÁXIMO COMÚN MÚLTIPLO


 (M.C.M.)

MÁXIMO COMÚN DIVISOR (M.C.D.)