TEMA: LA FILOSOFÍA
PROPÓSITO: conozco el significado de la
palabra filosofía, y su principal interrogante de la antropología filosófica
¿Quién soy? Haciendo un análisis del nombre propio.
ACTIVIDADES A REALIZAR: creación de decoración del
propio nombre con objeto con el que se identifiquen y copia de conclusiones.
EVALUACIÓN. ( auto, coe,meta)
Se les hará la siguiente pregunta ¿Qué preguntas crees que
trata de responder la Filosofía?
CONCLUSIONES
Después
escribiremos las conclusiones en el cuaderno: más que preguntarnos qué es la
filosofía como acumulación de conocimientos que otros dedujeron, vamos a
responder qué es filosofar que es la acción de pensar que todos podemos hacer y
qué es pensar? Entonces según Ortega y Gasset un filósofo español es: una
tarea, algo que el ser humano hace por algo y para algo
La filosofía no pretende
enseñar a hacer zapatos, pero es capaz de descubrir un interrogante más profundo por qué es conveniente fabricar
buenos zapatos. Sin filosofía no conoceríamos el "sentido" último de
la fabricación de zapatos, ni de nada.
La cuestión es: ¿para qué necesitamos un objeto que no sea útil? Bien. ¿Qué hay, por ejemplo, en nuestra sala de estar? Objetos que sirven para algo: sillas para sentarse, mesa, ceniceros, radiadores, etcétera. Pero también encontramos cuadros, esculturas, fotografías de parientes y amigos. ¿Para qué sirven todas estas cosas? ¿Qué se puede hacer con ellas? Aparentemente nada. ¿Para qué sirven? Para decorar. Aquí nos encontramos con un valor que no es inmediatamente útil, el decoro.» (Alejandro Llano).
El ser humano es un ser teórico-práctico: no se puede amputar. Para que su acción le satisfaga ha de ser fruto de una buena teoría. No hay nada más práctico que una buena teoría, es decir, una buena ciencia de porqués últimos. Ganar dinero es un porqué inmediato. Pero no es un porqué último. Por eso no podemos evitar la pregunta: ¿Por qué ganar dinero?
La cuestión es: ¿para qué necesitamos un objeto que no sea útil? Bien. ¿Qué hay, por ejemplo, en nuestra sala de estar? Objetos que sirven para algo: sillas para sentarse, mesa, ceniceros, radiadores, etcétera. Pero también encontramos cuadros, esculturas, fotografías de parientes y amigos. ¿Para qué sirven todas estas cosas? ¿Qué se puede hacer con ellas? Aparentemente nada. ¿Para qué sirven? Para decorar. Aquí nos encontramos con un valor que no es inmediatamente útil, el decoro.» (Alejandro Llano).
El ser humano es un ser teórico-práctico: no se puede amputar. Para que su acción le satisfaga ha de ser fruto de una buena teoría. No hay nada más práctico que una buena teoría, es decir, una buena ciencia de porqués últimos. Ganar dinero es un porqué inmediato. Pero no es un porqué último. Por eso no podemos evitar la pregunta: ¿Por qué ganar dinero?
En
definitiva nos ayuda a responder los interrogantes más profundos:
·
¿Quién soy?
·
¿Por qué vivir?
·
¿Por qué estudiar?
·
¿Qué sentido tiene todo
esto?
·
¿A dónde va mi vida?
·
¿De dónde salió el universo?
 (es decir 1) ; el siguiente las
(es decir 1) ; el siguiente las 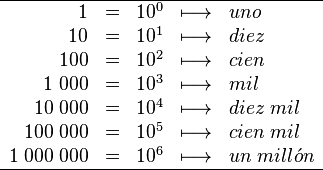


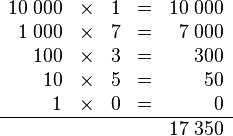




 .
.












