domingo, 28 de enero de 2018

SEMANA TRES MATEMÁTICAS

ENERO 29 A FEBRERO 2


Repaso de los sistemas de numeración Babilónico, Egipcio, Romano( para sexto A)  y con el maya también(para sexto B) y evaluación escrita.

TALLER Nº 3


1. Observar los videos del blog. Realizar en el cuaderno de matemáticas un breve comentario de cada uno de los videos de los sistemas de numeración vistos hasta el momento.
2. Observar el video: "El pato Donald en el país de las matemáticas" y hacer un resúmen del mismo en el cuaderno de geometría.




SISTEMA DE NUMERACIÓN DECIMAL


El sistema de numeración decimal, también llamado sistema decimal, es un sistema de numeración posicional en el que las cantidades se representan utilizando como base aritmética las potencias del número diez. El conjunto de símbolos utilizado (sistema de numeración arábiga) se compone de diez cifras : cero (0) - uno (1) - dos (2) - tres (3) - cuatro (4) - cinco (5) - seis (6) - siete (7) -ocho (8) y nueve (9).
Excepto en ciertas culturas, es el sistema usado habitualmente en todo el mundo y en todas las áreas que requieren de un sistema de numeración. Sin embargo hay ciertas técnicas, como por ejemplo en la informática, donde se utilizan sistemas de numeración adaptados al método del binario o el hexadecimal.
Al ser posicional, el sistema decimal es un sistema de numeración en el cual el valor de cada dígito depende de su posición dentro del número. Al primero corresponde el lugar de las unidades, el dígito se multiplica por 10^0 (es decir 1) ; el siguiente las decenas (se multiplica por 10); centenas (se multiplica por 100); etc.
\begin{array}{rcccl} \hline 1 & = & 10^0 & \longmapsto & uno \\ 10 & = & 10^1 & \longmapsto & diez \\ 100 & = & 10^2 & \longmapsto & cien \\ 1\; 000 & = & 10^3 & \longmapsto & mil \\ 10\; 000 & = & 10^4 & \longmapsto & diez \; mil \\ 100\; 000 & = & 10^5 & \longmapsto & cien \; mil \\ 1 \; 000\; 000 & = & 10^6 & \longmapsto & un \; mill\acute{o}n \\ \hline \end{array}
  • Ejemplo:
\begin{array}{rcl} 347 & = & 3 \cdot 100 + 4 \cdot 10 + 7 \cdot 1 \\ & = & 3 \cdot 10^2 + 4 \cdot 10^1 + 7 \cdot 10^0 \end{array}
otro ejemplo:
17\; 350 = 1 \cdot 10\; 000 + 7 \cdot 1\; 000 + 3 \cdot 100 + 5 \cdot 10 + 0 \cdot 1
o también:
\begin{array}{rcrcr} 10\; 000 & \times & 1 & = & 10\; 000 \\ 1\; 000 & \times & 7 & = & 7\; 000 \\ 100 & \times & 3 & = & 300 \\ 10 & \times & 5 & = & 50 \\ 1 & \times & 0 & = & 0 \\ \hline & & & & 17\; 350 \end{array}

Se puede extender este método para los decimales, utilizando las potencias negativas de diez, y un separador decimal entre la parte entera y la parte fraccionaria.
\begin{array}{lcccl} \hline \rm d\acute{e}cima & \longmapsto & 10^{-1} & = & 0,1 \\ \rm cent\acute{e}sima & \longmapsto & 10^{-2} & = & 0,01 \\ \rm mil\acute{e}sima & \longmapsto & 10^{-3} & = & 0,001 \\ \rm diezmil\acute{e}sima & \longmapsto & 10^{-4} & = & 0,0001 \\ \rm cienmil\acute{e}sima & \longmapsto & 10^{-5} & = & 0,00001 \\ \rm millon\acute{e}sima & \longmapsto & 10^{-6} & = & 0,000001 \\ \hline \end{array}
  • Ejemplo:
1,0243 = 1 \cdot 10^0 + 0 \cdot 10^{-1} + 2 \cdot 10^{-2}+ 4 \cdot 10^{-3} + 3 \cdot 10^{-4}
o también:
\begin{array}{lcrcl} 1 & \times & 1 & = & 1 \\ 0,1 & \times & 0 & = & 0,0 \\ 0,01 & \times & 2 & = & 0,02 \\ 0,001 & \times & 4 & = & 0,004 \\ 0,0001 & \times & 3 & = & 0,0003 \\ \hline & & & & 1,0243 \end{array}
  • El sistema de numeración romano es decimal, pero no-posicional:
IX = 9 \;
XI = 11 \; .

TALLER 4.

1. Escribe en numeración maya las siguientes cantidades:
a. 100      b. 10       c. 5         d. 30         e. 9          f. 16      g. 20      h. 70    i. 50

 j. 60         k. 18        l. 10       m. 13

2. escriba en cada caso el valor relativo y el valor absoluto de cada cifra resaltada en negrilla:
a. 8925             b. 1834003            c. 955         d. 3493         e. 89            f. 9981

g. 13805           h. 198322               i. 655555

3. Escriba la descomposición polinómica de cada número:

a. 5381        b. 495       c. 95748        d. 306       e. 499     f. 79576      g. 18743

h. 109748     i. 100

4. Este cuarto punto se dictará en el aula de clase. ( Escribir el número correspondiente a cada descomposición polinómica)

Publicado por en
Etiquetas:

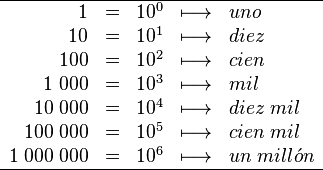
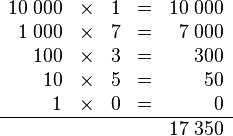
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)