DIBUJAR EN EL CUADERNO LAS CLASES SOCIALES DE LOS DIFERENTES PUEBLOS DE LA REGIÓN DE MESOPOTAMIA
lunes, 28 de mayo de 2018
SEMANA # 19 FILOSOFIA
TALLER LAS FORMAS Y LA MATERIA EN ARISTÓTELES
Aristóteles constata que la realidad está compuesta de una serie de cosas individuales que constituyen un conjunto de materia y forma. La «materia» es el material del que está hecha una cosa, y la «forma» son las cualidades específicas de la cosa. La «forma» de la gallina es precisamente aletear, y también cacarear y poner huevos. Así pues, la «forma» de la gallina son las propiedades específicas de la especie «gallina» o, dicho de otra manera, lo que hace que la gallina sea gallina. Cuando la gallina muere, y con ello deja de cacarear, la «forma» de la gallina deja de existir. Lo único que queda es la «materia» de la gallina pero entonces, ya no es una gallina.
Como ya he indicado, Aristóteles se interesaba por los cambios que tienen lugar en la naturaleza. En la (“materia” siempre hay una posibilidad de conseguir una determinada «forma». Podemos decir que la «materia» se esfuerza por hacer realidad una posibilidad de ser algo. Cada cambio que tiene lugar en la naturaleza es, según Aristóteles, una transformación de la materia de posibilidad a realidad
Mira este ejemplo de lo que decimos: Érase una vez un escultor que estaba agachado sobre un enorme bloque de granito. Todos los días daba martillazos y picaba la piedra enorme, y un día recibió la visita de un niño. «¿Qué estás buscando?», preguntó el niño. «Espera y verás», dijo el escultor. Al cabo de unos días el niño volvió. Para entonces el escultor había esculpido un hermoso caballo del bloque de granito. El niño lo miró asombrado, y luego se volvió al escultor y dijo: «¿Cómo podías saber que el caballo estaba ahí dentro?». Pues eso, ¿cómo podía saberlo? De alguna manera el escultor había visto la «forma» del caballo en el bloque de granito. Porque precisamente ese bloque de granito tenía una posibilidad inherente de transformarse en caballo. De esa manera, pensaba Aristóteles, todas las cosas de la naturaleza tienen una posibilidad de realizar o concluir en una determinada «forma».
- ¿Qué es la forma y la materia para Aristóteles?
- Escribe un ejemplo distinto al del texto sobre lo que es la forma y la materia para Aristóteles
- ¿Cuál sería la posibilidad o posibilidades de la materia de un huevo de la gallina? ( en qué se podría convertir)
domingo, 27 de mayo de 2018
SEMANA 19 MATEMÁTICAS EMILSE
MAYO 28 A JUNIO 1
Tipos de ángulos según su posición
- Ángulos consecutivos: Los ángulos consecutivos tienen en común un vértice y un lado.
- Ángulos adyacentes: Los ángulos adyacentes son ángulos consecutivos que tienen los lados no comunes en la misma recta.:
- Ángulos opuestos por el vértice: - Ángulos opuestos por el vértice: tienen el vértice común y sus lados están sobre las mismas rectas. Dos rectas que se cortan determinan dos parejas de ángulos opuestos por el vértice. Los ángulos opuestos por el vértice miden lo mismo.
- Ángulos opuestos por el vértice: - Ángulos opuestos por el vértice: tienen el vértice común y sus lados están sobre las mismas rectas. Dos rectas que se cortan determinan dos parejas de ángulos opuestos por el vértice. Los ángulos opuestos por el vértice miden lo mismo.
Dos rectas que se cortan reciben el nombre de secantes.
Nota: Los ángulos adyacentes son suplementarios.
Clases de ángulos según su suma
Según la suma de sus medidas dos ángulos pueden ser :
- Ángulos complementarios: - Dos ángulos son complementarios si su suma es igual a 90°.
- Ángulos suplementarios:- Dos ángulos son suplementarios si su suma es igual a 180°.
Ejemplos:
El complemento de un ángulo de 28° es un ángulo de 62°. Ya que 28° + 62° = 90°
El complemento de un ángulo 40° es un ángulo de 50°. Ya que 40° + 50° = 90°
El suplemento de un ángulo de 18° es un ángulo de 162°. Ya que 18° + 162° = 180°
El suplemento de un ángulo de 136° es un ángulo de 44°. Ya que 136° + 44° = 180°
- El truco está en acordarse que para calcular el ángulo complementario de uno o unos ángulos dados deberemos restarle a 90° su amplitud/es y para calcular el ángulo suplementario, habrá que restarle a 180° su amplitud/es.
ELABORACIÓN DE TALLER EN EQUIPO.
jueves, 24 de mayo de 2018
SEMANA #18. EDUCACIÓN ARTÍSTICA Y CULTURAL.
Tema Pixel art
El píxel es la unidad más pequeña y diminuta de una imagen digital y está presente en un inmensurable número para formar una imagen completa. Cada píxel es una unidad homogénea de color que en suma y con una importante variación de colores dan como resultado una imagen más o menos compleja. Los píxeles de una imagen son fácilmente observables cuando se procede a realizar un zoom sobre la misma ya que esto permite observar con mayor detenimiento los píxeles que han sido utilizados para componer la imagen. Todos los píxeles son cuadrados o rectangulares y pueden ser de color, blancos, negros o grises en diferentes tonalidades. Las combinaciones posibles de color son infinitas y han llegado a ser muy desarrolladas en comparación con las primeras imágenes digitales que carecían de suavidad y realidad.
(Recuperado de:... via Definicion ABC https://www.definicionabc.com/tecnologia/pixel.php
En un plano de dibujo, se trabaja en hojas cuadriculadas, donde cada cuadro representa un Pixel.
Objetivo: Identificar y Aplicar la técnica de dibujo con base al concepto de Pixel Art.
Actividad de clase:
Con base a la técnica trabajada a partir de las hojas cuadrículadas, realizar un diseño pixelado.
Sigue la cuadrícula y verás que es fácil hacerlo. Suerte!
lunes, 21 de mayo de 2018
SEMANA # 18 FILOSOFÍA
TEMA: CINE FORO LOS COLORES DELA MONTAÑA

PROPÓSITO: realizar un cine foro basado en la película los
colores de la montaña
colores de la montaña
ACTIVIDAD: realiza el siguiente
cuestionario.
1. Completa la siguientes espacios
La historia de Los colores de la montaña. Lee la siguiente
La historia de Los colores de la montaña. Lee la siguiente
sinopsis argumental y la información sobre la película y
complétala.
complétala.
Los colores de la montaña es la historia de
Manuel, de 9
años, quien tiene una _____pelota con la que juega al
_________
todos los días en el ______________. Sueña
con llegar a ser un gran __________.
Y el sueño parece que
se cumple cuando Ernesto, su ________, le regala un
______ nuevo. Pero un accidente _________ hace que el
balón caiga en un campo
minado. A pesar del _________,
Manuel decide no abandonar su balón. Convence a
Julián y
a Poca Luz, sus dos mejores ___________, para que juntos
lo rescaten. En
medio de las____________ y los juegos
infantiles, los signos de un conflicto
armado empiezan a
aparecer en la vida de los _________ de la vereda 'La
Pradera'
domingo, 20 de mayo de 2018
SEMANA 18 MATEMÁTICAS EMILSE
MAYO 21 AL 25
REPASO DE ÁNGULOS SEGÚN SU MEDIDA Y ELABORACIÓN DE TALLER EN EQUIPO REALIZANDO MEDICIONES,APLICADO AL TEMA
2.3- Ángulos obtusos
Un ángulo obtuso es un ángulo que mide más de 90° pero menos de 180°.
3- Algunas cosas importantes que debes saber
Los ángulos que miden más de 180° y menos de 360° se denominan ángulos cóncavos.
Los ángulos que miden 360° se denominan ángulos completos.
El ángulo nulo está formado por dos semirrectas coincidentes, por lo que su abertura es nula, es decir, 0°.
REPASO DE ÁNGULOS SEGÚN SU MEDIDA Y ELABORACIÓN DE TALLER EN EQUIPO REALIZANDO MEDICIONES,APLICADO AL TEMA
Definición de ángulo
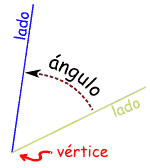
Se llama ángulo a la parte del plano delimitada por dos semirrectas que parten de un mismo punto llamado vértice. A cada semirrecta se le llama lado del ángulo.
Se llama ángulo a la parte del plano delimitada por dos semirrectas que parten de un mismo punto llamado vértice. A cada semirrecta se le llama lado del ángulo.
- Los lados del ángulo son las semirrectas que lo forman.
- El vértice del ángulo es el punto común que es origen de los lados.
Los tipos de ángulos son:
Agudo < 90°
Recto = 90°
Obtuso > 90°
Convexo < 180°
Llano = 180°
Cóncavo > 180°
Completo = 360°
Nulo = 0º
Agudo < 90°
Recto = 90°
Obtuso > 90°
Convexo < 180°
Llano = 180°
Cóncavo > 180°
Completo = 360°
Nulo = 0º
Hoy hablaremos de los ángulos agudo, recto y obtuso.
2- Tipos de ángulos según su medida
| Agudo < 90° | Recto = 90° | Obtuso>90° |
2.1- Ángulos rectos
Un ángulo recto es un ángulo que mide 90°. Si te das cuenta, en la esquina del ángulo hay un símbolo especial, una caja. Si ves ese símbolo, el ángulo es recto. No se suele escribir el 90°. Si ves la caja en la esquina ya te están diciendo que es un ángulo recto.
Un ángulo recto es un ángulo que mide 90°. Si te das cuenta, en la esquina del ángulo hay un símbolo especial, una caja. Si ves ese símbolo, el ángulo es recto. No se suele escribir el 90°. Si ves la caja en la esquina ya te están diciendo que es un ángulo recto.
Un ángulo recto puede estar en cualquier orientación o giro, lo que importa es que el ángulo interior sea 90°
2.2- Ángulos agudos
Un ángulo agudo es un ángulo que mide menos de 90°.
Un ángulo agudo es un ángulo que mide menos de 90°.
Acuérdate de fijarte en cuál de los dos ángulos es al que se refiere uno. Si el ángulo pequeño es menor que 90°, entonces ese es agudo.
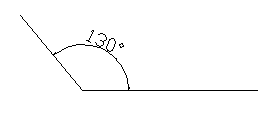
2.3- Ángulos obtusos
Un ángulo obtuso es un ángulo que mide más de 90° pero menos de 180°.
Acuérdate de fijarte en cuál de las dos partes es a la que se refiere uno. El ángulo más pequeño entre laslíneas es obtuso si mide entre 90° y 180°.
3- Algunas cosas importantes que debes saber
Los ángulos que miden 180° se denominan ángulos extendidos o llanos.
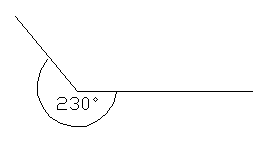
Los ángulos que miden más de 180° y menos de 360° se denominan ángulos cóncavos.
Los ángulos que miden 360° se denominan ángulos completos.
El ángulo nulo está formado por dos semirrectas coincidentes, por lo que su abertura es nula, es decir, 0°.
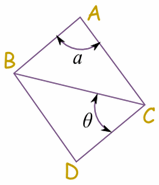
Los ángulos pueden nombrarse utilizando letras griegas. Por ejemplo:
4- Cómo medir ángulos usando el transportador
Medir un ángulo significa determinar su amplitud y, para hacerlo generalmente se utiliza el transportador.
Un transportador es un instrumento en forma circular o semicircular y graduado angularmente.
Los ángulos se miden en grados sexagesimales. Un grado corresponde a la medida del ángulo que se forma cuando una circunferencia se divide en 360 partes iguales.
Los grados indican la separación de los lados del ángulo. Mientras más separados están los rayos que forman el ángulo, mayor esla cantidad de grados que este mide.
4.1- Para medir ángulos utilizando el transportador semicircular debes:
1° Colocar el trazo recto del transportador sobre uno de los lados del ángulo.
1° Colocar el trazo recto del transportador sobre uno de los lados del ángulo.
2° Hacer que el punto medio de ese trazo coincida con el vértice del ángulo.
3° Observar el otro lado del ángulo y su valor según la escala angular del transportador. Si el ángulo está abierto hacia la izquierda debes fijarte en la escala externa y si está abierto hacia la derecha en la escala interna.
4.2- Para medir ángulos utilizando el transportador circular debes:
1° Colocar uno de los lados del ángulo frente al 0°.
1° Colocar uno de los lados del ángulo frente al 0°.
2° Hacer coincidir el centro de la circunferencia con el vértice del ángulo.
3° Observar el otro lado del ángulo y su valor según la escala angular del transportador.
martes, 15 de mayo de 2018
SEMANA # 17 FILOSOFÍA
1. Se hará hermenéutica de los siguientes
aforismos:
“El sabio no dice todo lo que piensa, pero siempre piensa todo lo que
dice”
“Nada hay en el entendimiento que antes no haya pasado por los sentidos”
“El ignorante afirma, el sabio duda y reflexiona”
“La inteligencia consiste no sólo en el
conocimiento, sino también en la destreza de aplicar los conocimientos en la
práctica”
2. Explicación
diferencias y semejanzas entre Aristóteles y platón en lo referente a:
diferencias
- Lo que
piensan acerca de los sentidos
- La forma en que escriben
- El lugar donde están las ideas o esencias de
las cosas
- Cómo se da el conocimiento por la razón o por
los sentidos
- Cuál es el verdadero mundo donde se obtiene el
conocimiento real
- La razón o alma ya llega con la información o
es tabula rasa
- Aristóteles afirma no hay nada en el
entendimiento que antes no haya pasado por los sentidos y platón podría
decir no hay nada en la naturaleza que antes no haya estado en el mundo de
las ideas
- Aristóteles entonces piensa que Platón duplicó
las cosas
- Sobre el cuerpo y alma una o dualidad
Concepción antropológica)
semejanzas
- Las cosas tienen esencias para uno está en el mundo
inteligible y el otro en las cosas
- Si queremos hacer ciencia ( conocimiento verdadero)
buscamos lo universal
- Existe razón o alma pero uno piensa que es tabula rasa y
otro ya trae la información del mundo de las ideas
3. observación de video https://youtu.be/3OlBRyeOZuQ
4. copia:
Platón dio la espalda al
mundo de los sentidos, volviendo la cabeza ante todo lo que vemos a nuestro
alrededor. (¡Quería salir de la caverna, quería contemplar el mundo eterno de
las Ideas!) Aristóteles hizo lo contrario. Se puso de rodillas en la tierra
para estudiar peces y ranas, amapolas y anémonas. Podríamos decir que Platón
sólo usaba su inteligencia; Aristóteles también usaba sus sentidos.
También en la forma en la
que escriben, se encuentra una gran diferencia entre ellos. Platón era un
poeta, un creador de mitos; los escritos de Aristóteles son áridos y minuciosos
como una enciclopedia. No obstante, se nota en mucho de lo que escribe que él
se basa en su estudio de la naturaleza. También en la época de Aristóteles la
filosofía era ante todo una actividad oral.
La gran importancia de
Aristóteles en la cultura europea se debe también, en buena medida, al hecho de
que fuera él quien creara el lenguaje profesional que las distintas ciencias
emplean hasta hoy en día. Fue el gran sistematizador que fundó y ordenó las distintas
ciencias.
No
hay ideas innatas
Platón deseaba encontrar
algo eterno e inmutable, en medio de todos los cambios. Encontró las Ideas
perfectas, que estaban muy por encima del mundo de los sentidos. Platón
opinaba, además, que las Ideas eran más reales que todos los fenómenos de la
naturaleza. Primero estaba la «idea de caballo», luego llegaban todos los
caballos del mundo de los sentidos galopando en forma de sombras en la pared de
una caverna. Esto quiere decir que la «idea de gallina» estaba antes que la
gallina y que el huevo.
Aristóteles pensaba que
Platón había dado la vuelta a todo. Estaba de acuerdo con su profesor en que el
caballo individual «fluye», y que ningún caballo vive eternamente. También
estaba de acuerdo en que el «molde de caballo» es eterno e inmutable. Pero la
«idea de caballo» no es más que un concepto que los seres humanos nos hemos
formado después de ver un cierto número de caballos. Eso quiere decir que la
«idea» o la «forma» de caballo no existen en sí. «Forma» del caballo es, para Aristóteles,
las cualidades del caballo o lo que hoy en día llamamos especie. Para ser más
preciso: con «forma» del caballo, Aristóteles quiere designar lo que es común
para todos los caballos. Y aquí no nos basta el ejemplo de las pastas, pues los
moldes de pastelería existen independientemente de esas determinadas pastas.
Aristóteles no pensaba que existieran tales moldes, que, por así decirlo,
estaban colocados en estantes fuera de la naturaleza. Para Aristóteles las
formas de las cosas son como las cualidades específicas de las cosas.
Esto quiere decir que
Aristóteles está en desacuerdo con Platón en que la Idea de «gallina» sea
anterior a la gallina. Lo que Aristóteles llama «forma de gallina», está
presente en cada gallina, como las cualidades específicas de la gallina; por ejemplo,
el hecho de que ponga huevos. De ese modo la propia gallina y la «forma» de
gallina son tan inseparables como el cuerpo y el alma.
Con esto hemos dicho lo
esencial sobre la crítica de Aristóteles a la teoría de las Ideas de Platón. Para
Platón, el mayor grado de realidad es lo que pensamos con la razón. Para
Aristóteles era igual de evidente que el mayor grado de realidad es lo que
sentimos con los sentidos. ( hasta aquí la copia)
Platón opina que todo lo
que vemos a nuestro alrededor en la naturaleza, son meros reflejos de algo que
existe de un modo más real en el mundo de las Ideas, y con eso también en el
alma del ser humano. Aristóteles opina exactamente lo contrario. Lo que hay en
el alma del ser humano, son meros reflejos de los objetos de la naturaleza; es
decir, la naturaleza es el verdadero mundo. Según Aristóteles, Platón quedó
«anclado» en una visión mítica del mundo, en la que los conceptos del hombre se
confunden con el mundo real. Aristóteles señaló que no existe nada en la mente
que no haya estado antes en los sentidos, y Platón podría haber dicho que no hay
nada en la naturaleza que no haya estado antes en el mundo de las Ideas. En ese
sentido, opinaba Aristóteles, Platón «duplicaba el número de las cosas».
Explicaba cada caballo haciendo referencia a «la idea» de caballo. ¿De dónde
viene la «idea de caballo»? ¿Existe acaso también un tercer caballo, del que la
«idea de caballo» es un mero reflejo? Podría pensar Aristóteles Aristóteles
pensó que todo lo que tenemos dentro de pensamientos e ideas ha entrado en
nuestra conciencia a través de lo que hemos visto y oído. Pero también tenemos
una razón innata con la que nacemos. Tenemos una capacidad innata para ordenar
todas nuestras sensaciones en distintos grupos y clases. Así surgen los
conceptos «piedra», «planta», «animal» y «hombre». Así surgen los conceptos
«caballo», «cangrejo» y «canario». Aristóteles no negó que el hombre tuviera
una inteligencia innata. Al contrario, según Aristóteles es precisamente la
razón la que constituye la característica más destacada del ser humano. Pero
nuestra inteligencia está totalmente vacía antes de que sintamos algo. Por lo
tanto el ser humano no puede nacer con idea alguna.
SEMANA #17. EDUCACIÓN ARTÍSTICA Y CULTURAL.
Observaciones: Se aplaza la actividad, para el grado 6°1, debido a que el lunes 14 de mayo fue festivo y para el grado 6º2 debido a que el miércoles 16 de mayo fue jornada institucional sobre la Excelencia Educativa.
Este año, el ‘Día E’ se realizará el 16 de mayo, según la Resolución 7182 de 2018, y será un espacio propicio para hacer un balance de los avances que en materia de calidad educativa ha tenido el país.
Para guiar esta jornada se definió el ISCE, que se conforma de cuatro componentes: progreso, desempeño, eficiencia y ambiente escolar, para que todos los colegios del país tengan un marco común de discusión.
- Progreso: mide mejoría del colegio en relación con el año inmediatamente anterior.
- Eficiencia: busca balancear el puntaje obtenido en desempeño. Mide que todos los estudiantes alcancen los logros propuestos en el grado escolar. La calificación será según el número de estudiantes que son aptos para aprobar los grados del ciclo evaluado.
- Desempeño: incentiva a aquellos con los mejores resultados en las pruebas Saber.
- Ambiente Escolar: revisa en qué contexto se están desarrollando las clases que están recibiendo todos los estudiantes.
https://www.mineducacion.gov.co/1759/w3-article-369401.html
lunes, 14 de mayo de 2018
domingo, 13 de mayo de 2018
SEMANA 17 MATEMÁTICAS EMILSE
14 AL 18 DE MAYO
Los ángulos se pueden medir en grados.
Hay 360 grados en una vuelta completa (un círculo completo).
(También se pueden medir ángulos en radianes)

Así de grande es 1 grado
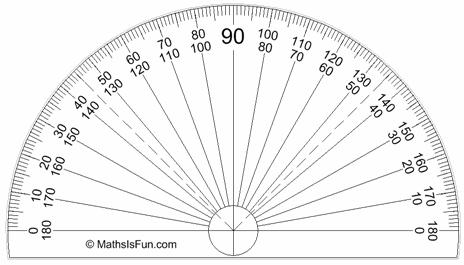
Normalmente los transportadores miden ángulos de 0° a 180°
Grados (ángulos)
Los ángulos se pueden medir en grados.
Hay 360 grados en una vuelta completa (un círculo completo).
(También se pueden medir ángulos en radianes)
Grados (ángulos)
(Nota: "grados" también pueden ser de temperatura, pero aquí sólo hablamos de ángulos)
El símbolo de grado: °
Se usa un pequeño círculo ° después del número para indicar grados.
Por ejemplo 90° significa 90 grados
Un grado
Así de grande es 1 grado
Un círculo completo
Un cículo completo son 360°
Medio círculo son 180°
(esto se llama ángulo llano)
Un cuarto de círculo son 90°
(y se llama ángulo recto) | 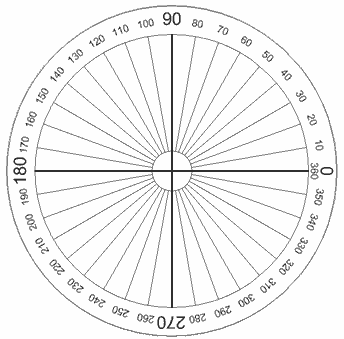 |
¿Por qué son 360? Probablemente porque antiguamente había calendarios (por ejemplo el persa) que tenían 360 días por año, así que cuando miraban las estrellas veían que giraban alrededor de la Estrella Polar un grado cada día.
|
Midiendo grados
Muchas veces medimos grados usando un transportador:
Normalmente los transportadores miden ángulos de 0° a 180°
 |
También hay transportadores de vuelta completa.
Pero no son tan comunes porque son grandes y no valen para nada especial.
Nombres de los ángulosSegún aumenta el ángulo, el nombre va cambiando
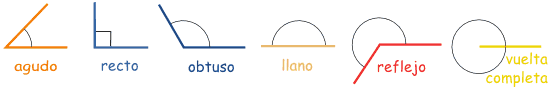 Cuidado con las medidas
Marcar ángulos
| |||||||||||||||||||||||||
martes, 8 de mayo de 2018
SEMANA #16. EDUCACIÓN ARTÍSTICA Y CULTURAL.
Observación: El grado 6°1 inicia con el ejercicio. El grado 6°2 concluye el ejercicio, termina de colorear.
Tema:Diseños Geométricos con base a hojas cuadriculadas.
Objetivo: desarrollar la capacidad espacial a partir de la construcción de un diseño geométrico, seleccionar libremente los colores para el diseño, aplicar el color parejo a la superficie.
Tema:Diseños Geométricos con base a hojas cuadriculadas.
Objetivo: desarrollar la capacidad espacial a partir de la construcción de un diseño geométrico, seleccionar libremente los colores para el diseño, aplicar el color parejo a la superficie.
Con base a la explicación de la docente en clase, ubica un punto en el centro de la hoja, dibuja una cruz de 2 cuadros de ancho, colorea del color que desees, alrededor de la vertical y horizontal de la cruz deja cuatro cuadros de espacio y une toda la forma en escalera de a dos cuadros del bloc, continúa así alrededor de cada forma hasta llegar a los extremos de la hoja.
Colorea con colores claros al lado de colores oscuros para que exista contraste, aplica el color saturado o sea evita colorear suave.
lunes, 7 de mayo de 2018
SEMANA 17 EL UNIVERSO
COPIAR EN EL CUADERNO LOS DIFERENTES ELEMENTOS DEL UNIVERSO
HACER UN MAPA CONCEPTUAL SOBRE EL ORIGEN DEL UNIVERSO
HACER UN MAPA CONCEPTUAL SOBRE EL ORIGEN DE LA TIERRA
HACER UN MAPA CONCEPTUAL SOBRE EL ORIGEN DE LA TIERRA
SEMANA # 16 FILOSOFÍA
ARISTÓTELES
ARISTÓTELES
(384
– 322 a de C)
Este
filósofo, estudió en la Academia de Platón, cuyas ideas rebatió.
La Filosofía
de Aristóteles es monumental, por la cantidad de temas que trata: ética,
metafísica, lógica y poética entre otros; así como por la profundidad y riqueza
de sus ideas. Aristóteles superó la dualidad platónica entre el mundo
inteligible y el mundo sensible afirmando que las cosas tiene tres elementos
que se pueden distinguir: la sustancia, la esencia y los accidentes. La
sustancia es aquello de lo que decimos algo. La esencia es aquello por lo cual
la sustancia es lo que es, y no otra cosa; y los accidentes son características
de la sustancia que no alteran la esencia. Los conceptos de materia y forma son
fundamentales en la filosofía aristotélica. La materia es aquello de lo que
están hechas las cosas. La forma es su misma esencia, lo que las define. Para
explicar el movimiento se valió de los conceptos de acto y potencia. Cuando nos
referimos a una sustancia, podemos hablar de lo que ella es en un momento
determinado (acto), o de lo que
puede llegar a ser (potencia).
1.
Pegue el texto en el cuaderno y responde las
siguientes preguntas.
2.
¿Cuáles son los temas que trata Aristóteles
en su filosofía?
3.
Define según el texto los siguientes términos.
SUSTANCIA, ESENCIA, ACCIDENTES, MATERIA, FORMA.
4.
¿Qué es acto y potencia para Aristóteles?
5.
Según lo que afirma Aristóteles sobre acto y
potencia, realiza un dibujo de ti mismo donde representes
quien eres en el presente (ACTO) y quien deseas ser en el futuro ( PONTENCIA)
6.
https://youtu.be/PM0V9IuYDj8
metafísica de Aristóteles
Suscribirse a:
Comentarios (Atom)