VIDEO "EL PATO DONALD EN EL PAÍS DE LAS MATEMÁTICAS"
Observar el video y extraer lo más relevante. Hacer un resúmen y socializar en el aula de clase.
GEOMETRÍA
pirámides y monumentos.La geometría como palabra tiene dos raíces griegas: geo = tierra y metrón = medida; o sea, significa"medida de la tierra". Su origen, unos tres mil años antes de Cristo, se remonta al Medio Oriente, enparticular al Antiguo Egipto, en que se necesitaba medir predios agrarios y en la construcción de
La civilización babilónica fue una de las primeras culturas en incorporar el estudio de la geometría.
La geometría surgió del estudio de los primeros matemáticos de la historia sobre problemas como las medidas de un campo o de un objeto. En el antiguo Egipto surgió una geometría observacional o empírica que provenía de la observación de los objetos. Esta geometría primigenia más adelante fue reformulada y elaborada por los griegos y es la geometría que hoy conocemos.
La Geometría trata sobre las formas y sus propiedades.
Los dos temas más comunes son:  | Geometría Plana (sobre formas planas como líneas rectas, círculos y triángulos... formas que se pueden dibujar en un trozo de papel) |
 | Geometría Sólida (sobre objetos tridimensionales como cubos y pirámides). |
Pitágoras
Euclides.
Puntos, segmentos, rectas y planos
El PUNTO es una «figura geométrica» adimensional: no tiene longitud, área, volumen, ni otro ángulo dimensional. No es un objeto físico. Describe una posición en el espacio, determinada respecto de un sistema de coordenadas preestablecido.
A los puntos se les suele nombrar con una letra mayúscula: A, B, C, etc.
El concepto de punto, como ente geométrico, surge en la antigua concepción griega de la geometría, compilada en Alejandría por Euclides en su tratado Los Elementos.
SEGMENTO
Un segmento, en geometría, es un fragmento de recta que está comprendido entre dos puntos.
ó también
Segmento es la porción de recta limitada por dos puntos, llamados extremos.
Este es el Segmento AB
LA RECTA
En geometría euclidiana, la recta o línea recta, es el ente ideal que se extiende en una mismadirección, existe en una sola dimensión y contiene infinitos puntos; está compuesta de infinitos segmentos (el fragmento de línea más corto que une dos puntos). También se describe como la sucesión continua e indefinida de puntos en una sola dimensión, o sea, no posee principio ni fin.
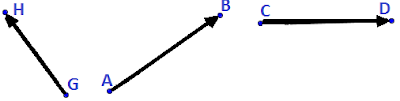
La Recta se nombra con una letra Minúscula o dos Mayúsculas y se lee la recta AB, la recta HG y la recta m.
LA SEMIRECTA
La Semirecta se nombra con dos Mayúsculas y se lee la Semirecta AB, la Semirecta HG.
EL PLANO
En geometría, un plano es el ente ideal que sólo posee dos dimensiones, y contiene infinitos puntos y rectas; es uno de los entes geométricos fundamentales junto con el punto y la recta.
Los planos suelen nombrarse con una letra del alfabeto griego: Alfa (α), Beta (β), Theta (θ), Fi (φ) entre otras
SEMIPLANO
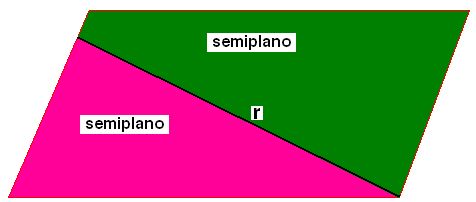
Si tenemos un plano y una recta en ese plano, la recta divide al plano en dos partesllamadas semiplanos.
Plano: 
Recta: r
Recta: r
Spl(r, A): se lee "semiplano de borde r que contiene al punto A"
Spl(r, B): se lee "semiplano de borde r que contiene al punto B"
La recta r ha creado dos semiplanos.
A cada zona en la que ha sido dividido el plano se le puede llamar región, porción de plano, banda, además de semiplano.
A la recta que divide a un plano en dos regiones o semiplanos se la conoce también con el nombre de frontera o recta frontera.
A la recta que divide a un plano en dos regiones o semiplanos se la conoce también con el nombre de frontera o recta frontera.
LÍNEAS PARALELAS
Las líneas que situadas en el mismo plano no se tocan por mucho que las prolonguemos son líneas paralelas:
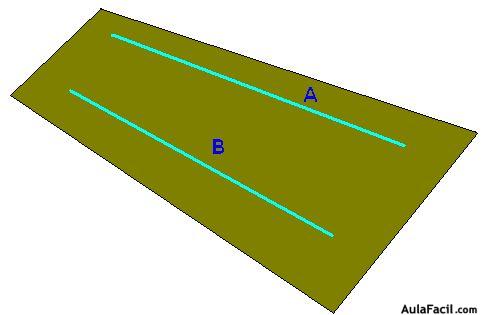
Las rectas A y B son paralelas. Las vías del tren son paralelas. En todos los puntos, las distancias entre ambas líneas es siempre la misma.
Perpendiculares
Simplemente significa en ángulos rectos (90°) con.
La línea roja es perpendicular a la azul en estos dos casos:
 |  |
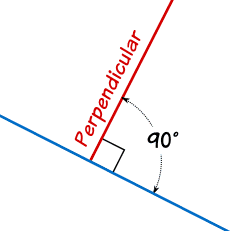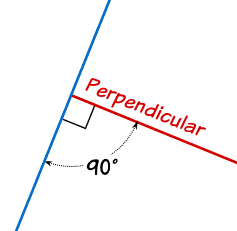(La cajita en la esquina significa "en ángulos rectos", así que no hacía falta poner también que son 90°, ¡pero queríamos hacerlo!)
Paralelas
Dos líneas son paralelas si siempre están a la misma distancia (se llaman "equidistantes"), y no se van a encontrar nunca. (También apuntan en la misma dirección). Sólo recuerda:
Siempre la misma distancia y no se encuentran nunca.
La línea roja es paralela a la azul en estos dos casos:
 |  | |||
Ejemplo 1
|
Ejemplo 2
Curvas paralelas
Las curvas también pueden ser paralelas cuando están siempre a la misma distancia (se llaman "equidistantes"), y nunca se encuentran. Como las vías de un tren.
La curva roja es paralela a la azul en los dos casos:
|
No hay comentarios:
Publicar un comentario