CLASES DE FRACCIONARIOS
1- Tipos de fracciones
Debes recordar que existen distintos tipos de fracciones:
- Fracción igual a la unidad
- Fracción propia
- Fracción impropia
- Fracciones decimales
- Fracciones equivalentes
- Fracciones irreducibles
- Fracciones inversas
- Fracción propia
- Fracción impropia
- Fracciones decimales
- Fracciones equivalentes
- Fracciones irreducibles
- Fracciones inversas
2- Fracción igual a la unidad
Es aquella fracción donde el numerador y el denominador son iguales.
Por ejemplo:
2 , 5 , 6 , 10
2 5 6 10
2 5 6 10
Al representar la fracción gráficamente tenemos:
Ejemplo:
3- Fracciones propias
Las fracciones propias son aquellas cuyo numerador es menor que el denominador. Su valor es menor que la unidad ya que se ubica entre cero y uno en la recta numérica.
Por ejemplo:
1 , 1 , 3 , 4 .
3 6 4 8
3 6 4 8
Al representar la fracción gráficamente tenemos:
Ejemplo:3/4
4- Fracciones impropias
Las fracciones impropias son aquellas cuyo numerador es mayor que el denominador. Su valor es mayor que 1.
Al representar la fracción gráficamente tenemos:
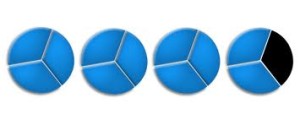
Ahora veamos cómo escribir las fracciones impropias desde las gráficas:
Aquí tenemos cuatro unidades divididas en tres partes, y hemos tomado 3 unidades y dos partes más, es decir, tenemos 11/3.
En toda fracción igual o mayor que la unidad; se reconoce por tener el numerador igual o mayor que el denominador
Una fracción impropia es igual o mayor que la unidad; por consiguiente, puede convertirse en número mixto (formado por un entero seguido de una fracción propia).
Para convertir una fracción impropia en número mixto se divide el numerador entre el denominador; el cociente será el entero y la fracción estará integrada por el residuo y el mismo denominador.
Si se tienen dos fracciones: 
con b y d 
0, al compararlas, se determina cuál de las tres relaciones siguientes se cumple:
con b y d 0, al compararlas, se determina cuál de las tres relaciones siguientes se cumple:
5. Número mixto
Las fracciones impropias se pueden escribir como numero mixto. El número mixto o fracción mixta está compuesto de un número entero y una fracción propia.
En el ejemplo anterior tenemos:
a) Para poder transformar una fracción impropia en número mixto lo que debemos hacer es:
Dividir el numerador por el denominador. El cociente o resultado de esa operación es el entero del número mixto y el resto el numerador de la fracción, siendo el denominador el mismo.
Ejemplo: en la fracción 8 / 5
Por tanto: 1 es el número natural y 3 es el numerador de la fracción y el denominador no cambia, es decir 5.
8
|
3
| ||
----
|
=
|
1
|
----
|
5
|
5
|
b) Para poder transformar un número mixto a fracción impropia lo que debemos hacer es:
El numero natural se multiplica por el denominador y se suma el numerador.
Ejemplo: en la fracción:
¿Cómo cambiar un número de mezcla a una fracción impropia?
- Multiplica el nombre por el número entero.
- Al resultado, sumale el numerador.
- Coloca este número sobre el denominador original.
Ejemplo 1
Ejemplo 2
6. Fracciones decimales
Una fracción decimal es aquella que tiene por denominador la unidad seguida de ceros: 10, 100, 1000. Ejm:
A- ¿Cómo se escribe una fracción decimal en forma de número decimal?
Para escribir un fracción decimal en forma de número decimal, se escribe el numerador y se separan con una coma, hacia la derecha, tantas cifras decimales como ceros tenga el denominador. si es necesario se añaden ceros.
Ejemplo 1:
Ejemplo 2:
Otros ejemplos:
B- ¿Cómo se escribe un número decimal en forma de fracción decimal?
Para escribir un número decimal en forma de fracción decimal, se escribe como numerador de la fracción el número decimal sin coma, y como denominador, la unidad seguida de tantos ceros como cifras decimales tiene el número decimal.
Ejemplos:
0,05= 5/100
2,354=2354/1000
14,5= 145/10
7. Fracciones equivalentes
Para escribir un número decimal en forma de fracción decimal, se escribe como numerador de la fracción el número decimal sin coma, y como denominador, la unidad seguida de tantos ceros como cifras decimales tiene el número decimal.
Ejemplos:
0,05= 5/100
2,354=2354/1000
14,5= 145/10
7. Fracciones equivalentes
Dos fracciones son equivalentes cuando tienen el mismo valor decimal. Las fracciones equivalentes representan la misma parte de una unidad o entero.
Si las representamos en la recta numérica, corresponden al mismo punto.
Ejemplo:
Si lo graficamos tenemos:
Esta tarta representa la fracción 12
Esta tarta representa la fracción 36
Esta tarta representa la fracción 48
¿Por qué son lo mismo? Porque cuando multiplicas (amplificas) o divide (simplificas) a la vez arriba y abajo por el mismo número, la fracción mantiene su valor. La regla a recordar es:
Para comprobar si dos fracciones son equivalentes, se multiplican sus términos en cruz. Si los productos obtenidos son iguales, las fracciones son equivalentes.
Por ejemplo:
34 y 45 ⇒ 3 x 5 = 4 x 4 ⇒ 15 = 16
Si las representamos en la recta numérica, corresponden al mismo punto.
Ejemplo:
Las fracciones equivalentes son fracciones que representan la misma cantidad, aunque parezcan diferentes.
Vamos a ver este ejemplo:
¿Te parece que estas fracciones representan la misma cantidad? ¿O son todas diferentes?
Lo vemos con las siguientes imágenes:
- Dividimos la tarta en tantos trozos como marque el denominador.
- Tomamos tantos trozos (la parte coloreada) como marque el numerador.
Esta tarta representa la fracción Esta tarta representa la fracción Esta tarta representa la fracción
Las tres fracciones son fracciones equivalentes porque representan la misma cantidad de tarta.
¿Cómo podemos saber si dos fracciones son equivalentes? Por el método de la multiplicación en cruz.
SEGUNDO EJEMPLO:
¿Por qué son lo mismo? Porque cuando multiplicas (amplificas) o divide (simplificas) a la vez arriba y abajo por el mismo número, la fracción mantiene su valor. La regla a recordar es:
¡Lo que haces a la parte de arriba de la fracción también lo tienes que hacer a la parte de abajo!
Para comprobar si dos fracciones son equivalentes, se multiplican sus términos en cruz. Si los productos obtenidos son iguales, las fracciones son equivalentes.
Por ejemplo:
Es método consiste en multiplicar el cruz las dos fracciones:
numerador1denominador1 y numerador2denominador2 ⇒
numerador1×denominador2=denominador1×numerador2
¿Son fracciones equivalentes las siguientes fracciones?
25 y 1025 ⇒ 2 x 25 = 5 x 10 ⇒ 50 = 50
SÍ son fracciones equivalentes
NO son fracciones equivalentes
es más largo que el de 
por consiguiente:
y 
Ambas fracciones se localizan en rectas numéricas de la misma longitud, como las de la siguiente página.
Los segmentos que determinan ambas fracciones son de igual tamaño; Entonces son equivalentes:
1. Al comparar dos fracciones utilizando la recta numérica, será mayor la que se encuentre a la derecha.
2. Si dos fracciones se ubican en el mismo punto sobre la recta numérica, se denominan fracciones equivalentes.
No hay comentarios:
Publicar un comentario